- Регистрация
- 7 Июл 2023
- Сообщения
- 2
Всем ку, многие задавались вопросом как получить единичный вектор направления взгляда.
Можно реализовать это более простым способом:
Из координат местоположения целевого блока отнять текущее местоположение глаз игрока, таким образом мы получаем вектор.
Далее нам нужно найти величину этого вектора, делается это тоже просто с помощью функции "Получить расстояние между 2 местоположениями".
Теперь делим X, Y, Z нашего вектора на значение расстояния.
Все, вектор у нас найден.
Но у такого способа имеются минусы, конкретно его неточность, которая проявляется на ближней дистанции и почти невилируется с отдалением. Связано это с тем, что местоположение целевого блока является координатой, как ни странно, блока. Т.е если вы в притык будете смотреть на блок, то вектор будет направлен в угол этого блока, получается что вектор будет искажен где-то на 45 градусов.
Поэтому нужны синус и косинус, благо мы можем получить yaw и pitch положения камеры игрока.
Положение камеры игрока во многих играх, я хз в какой это не так. Задается с помощью поворотов.
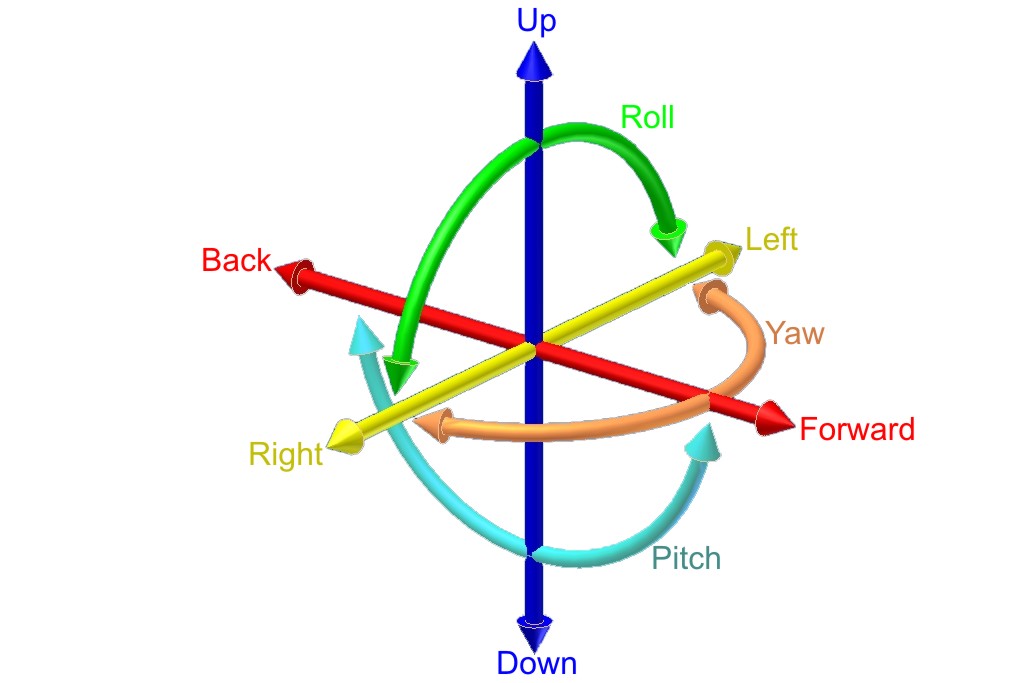
Как видите есть еще один способ поворота, называемый roll. Но по сути его можно заменить с помощью двух оставшихся.
Очень важна поочередность этих поворотов, то есть если первым делом повернем камеру по pitch то результат будет отличаться от способа с первым поворотом по yaw. Исправить это можно с помощью задания поворота кватернионами, но это не щас не важно, я сам хз как они работают.
Перейдем к теоретической реализации функций синуса и косинуса в коде.
Искать их мы будем с помощью ряда маклорена
Ссылка на разложение других функций


Где X это радианы, из градусов мы можем их получить с помощью формулы s*pi/180, где s это градусы.
Для приемлемой точности косинуса и синуса можно продолжить ряды до 6-7 члена включительно.
Далее не сложно догадаться как реализовать это в коде.
Мы создаем переменную, присваиваем ей значение в градусах, используя деление и умножение переводим в радианы.
Далее создаем копию нашей переменной, копию1 умножаем на саму себя, и создаем еще одну копию2. копия2 = x^2
Теперь, в случае с синусом, умножаем копию1 на оргинал, это получается x^3. Вычитаем из оригинала копию1 деленную на факториал 3(все факториалы заранее посчитаем в калькуляторе). копию1 умножаем на копию2. Прибавляем копию1 деленную на факториал 5. И так далее.
Теперь мы можем используя функции sin(x) и cos(x) найти вектор взгляда и делать с ним ВСЯКОЕ.
Вот формулы получения вектора.
x = cos(yaw)*cos(pitch)
y = sin(yaw)*cos(pitch)
z = sin(pitch)
Геометрически это можно объяснить так:
Сперва делается поворот по yaw, он ограничен от -90 до 90 градусов - смотреть в землю или в небо.
Если представить это на двумерной плоскости
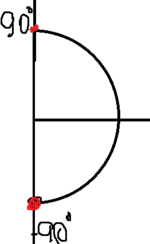
То можно видеть что максимальную горизонтальную дальность расстояния(хз как выразиться) мы получаем когда угол равен 0. cos(0)=1.
То есть мы должны будем умножить наш вектор полученный с yaw на эту длину.
Возможно при реализации будут какие-то баги, покрутите там углы.
Для реализации sin можете использовать уже готовый cos с помощью этих формул.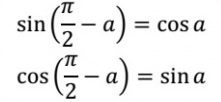
На самом деле не знаю будет ли кому-то от этого польза. Возможно те кому это надо уже нашли решение, те кому не надо - не будут даже вникать, поэтому без точной реализации в коде для них этот гайд бессмысленный.
Можно реализовать это более простым способом:
Из координат местоположения целевого блока отнять текущее местоположение глаз игрока, таким образом мы получаем вектор.
Далее нам нужно найти величину этого вектора, делается это тоже просто с помощью функции "Получить расстояние между 2 местоположениями".
Теперь делим X, Y, Z нашего вектора на значение расстояния.
Все, вектор у нас найден.
Но у такого способа имеются минусы, конкретно его неточность, которая проявляется на ближней дистанции и почти невилируется с отдалением. Связано это с тем, что местоположение целевого блока является координатой, как ни странно, блока. Т.е если вы в притык будете смотреть на блок, то вектор будет направлен в угол этого блока, получается что вектор будет искажен где-то на 45 градусов.
Поэтому нужны синус и косинус, благо мы можем получить yaw и pitch положения камеры игрока.
Положение камеры игрока во многих играх, я хз в какой это не так. Задается с помощью поворотов.

Как видите есть еще один способ поворота, называемый roll. Но по сути его можно заменить с помощью двух оставшихся.
Очень важна поочередность этих поворотов, то есть если первым делом повернем камеру по pitch то результат будет отличаться от способа с первым поворотом по yaw. Исправить это можно с помощью задания поворота кватернионами, но это не щас не важно, я сам хз как они работают.
Перейдем к теоретической реализации функций синуса и косинуса в коде.
Искать их мы будем с помощью ряда маклорена
Ссылка на разложение других функций


Где X это радианы, из градусов мы можем их получить с помощью формулы s*pi/180, где s это градусы.
Для приемлемой точности косинуса и синуса можно продолжить ряды до 6-7 члена включительно.
Далее не сложно догадаться как реализовать это в коде.
Мы создаем переменную, присваиваем ей значение в градусах, используя деление и умножение переводим в радианы.
Далее создаем копию нашей переменной, копию1 умножаем на саму себя, и создаем еще одну копию2. копия2 = x^2
Теперь, в случае с синусом, умножаем копию1 на оргинал, это получается x^3. Вычитаем из оригинала копию1 деленную на факториал 3(все факториалы заранее посчитаем в калькуляторе). копию1 умножаем на копию2. Прибавляем копию1 деленную на факториал 5. И так далее.
Теперь мы можем используя функции sin(x) и cos(x) найти вектор взгляда и делать с ним ВСЯКОЕ.
Вот формулы получения вектора.
x = cos(yaw)*cos(pitch)
y = sin(yaw)*cos(pitch)
z = sin(pitch)
Геометрически это можно объяснить так:
Сперва делается поворот по yaw, он ограничен от -90 до 90 градусов - смотреть в землю или в небо.
Если представить это на двумерной плоскости

То можно видеть что максимальную горизонтальную дальность расстояния(хз как выразиться) мы получаем когда угол равен 0. cos(0)=1.
То есть мы должны будем умножить наш вектор полученный с yaw на эту длину.
Возможно при реализации будут какие-то баги, покрутите там углы.
Для реализации sin можете использовать уже готовый cos с помощью этих формул.
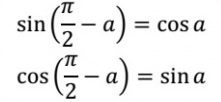
На самом деле не знаю будет ли кому-то от этого польза. Возможно те кому это надо уже нашли решение, те кому не надо - не будут даже вникать, поэтому без точной реализации в коде для них этот гайд бессмысленный.