Версия гайда: 1.2 (31.10.23)
Вектор взгляда может пригодиться, если вы хотите запускать снаряд в направлении взгляда игрока и спавнить снаряд перед лицом игрока, чтобы снаряд не столкнулся с игроком который его запустил. Также необходим для рейкаста (перемещения по лучу взгляда в основном для проверки пересечения/близости луча взгляда и сущности/блока).
Для понимания потребуются некоторые знания из тригонометрии, поэтому в первой части я расскажу про тригонометрическую окружность, синус и косинус. Если уверен в своих знаниях - пропускай её.
Часть I. Начала тригонометрии.
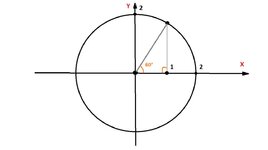
Тригонометрическая окружность - это единичная окружность (окружность с радиусом 1) с центром в начале координат.
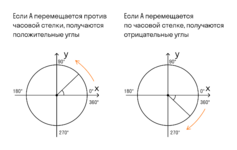
Какой угол (по величине) показан на правой окружности?
Возьмём единичную окружность, отметим на ней случайную точку P.
Проведём отрезок PA параллельно оси X, точка A лежит на оси Y.
Проведём отрезок PB параллельно оси Y, точка B лежит на оси X.
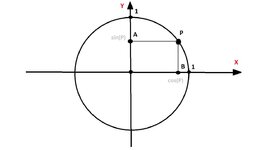
Синус - координата точки A на оси Y.
Косинус - координата точки B на оси X.
Т.е синус и косинус - это просто координаты любой точки, лежащей на единичной окружности.
Синус - координата на вертикальной оси, косинус - на горизонтальной оси (если оси расположены так как на рисунке).
Но что если радиус окружности не равен 1?
С изменением радиуса окружности пропорциоонально изменяются и координаты точки.
Чему равен косинус этого угла?
Часть II. Что такое вектор взгляда?
Вектор - это отрезок, имеющий направление, т.е начало и конец.

Единичный вектор - это вектор, длина которого равна 1.
Координатами вектора являются значения, сместившись на которые из начальной точки вектора (т.е прибавив их к координатам точки начала), мы окажемся в конечной точке вектора. Если начало вектора находится в начале координат, координаты вектора и координаты его конечной точки совпадают. Если начало не находится в начале координат, то чтобы найти координаты вектора нужно от координат конечной точки отнять координаты начальной.
Пример 1: есть вектор AB: A(0; 0), B(1; 3). Тогда AB{1-0; 3-0} = AB{1; 3}.
Пример 2: есть вектор CD: C(1; 1), D(-2; 3). Тогда CD{-2-1; 3-1} = CD{-3; 2}.
Вектор взгляда - это единичный вектор в трёхмерном пространстве, имеющий координаты, сместившись на которые точка будет находиться на луче взгляда.
Другими словами,
Вектор взгляда - это координаты для осей XYZ, на которые нужно сместиться, чтобы пройти единицу расстояния в направлении взгляда.

Часть III. Как получить вектор взгляда?
Получить вектор взгляда - значит найти координаты на которые нужно сместиться по осям XYZ, чтобы пройти единицу расстояния в направлении взгляда.
Для начала получим YAW и PITCH, вытащив значения из "Игровое значение" -> "Текущее направление взгляда".
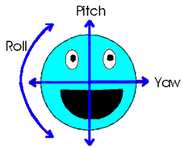
PITCH и YAW измеряются в градусах.
PITCH - это поворот вниз-вверх
- Отсчёт: -Y (90°) +Y (-90°) (-90° .. 90°).
YAW - это поворот влево-вправо
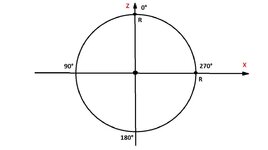
- Отсчёт: +Z (0°/360°) -X (90°) -Z (180°) +X (270°) (0° .. 360°).
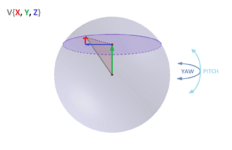
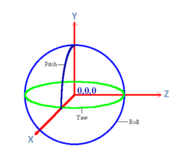
Так как длина вектора взгляда равна 1 (не меняется), набор всех возможных точек (концов векторов) образуют сферу (т.к сфера это по определению набор равноудалённых точек в трёхмерном пространстве).
На этой сфере PITCH - широта, а YAW - долгота (если вам это как-то поможет).
Рассмотрим PITCH (широту) на плоскости YA (см левую часть).
A - луч, который может лежать на оси X или Z, а может и не лежать, его местоположение зависит от YAW. Смотря на предыдущую картинку несложно представить, как эта полуокружность вращается вокруг оси Y с изменением YAW.
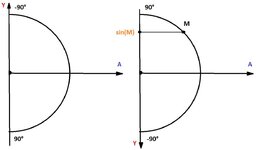
Для удобства перевернём картинку (см. правую часть). На полуокружности возможных значений PITCH находится точка M - случайное значение PITCH. Найдём значение синуса. Как можно видеть, оно лежит на перевёрнутой оси Y. Поэтому, для нахождения координаты Y вектора, его нужно домножить на -1 (это понятно ещё отсюда: "-Y (90°) +Y (-90°)" - в майнкрафте "вверх" это под отрицательным углом)
Итак, координата Y вектора взгляда найдена: -sin(pitch)
Теперь найдём точку косинуса, а точку sin(M) обозначим буквой P.
Можно заметить что длина отрезка PM = cos(M) = cos(pitch).
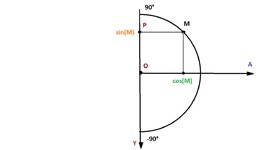
PM - это радиус окружности, которая получится на сечении сферы плоскостью XZ (горизонтальной плоскостью) в точке Y равной P. Сечение это то, что находится в секущей плоскости.
Фиолетовым выделена окружность, которая получится на сечении. Это окружность всех возможных значений YAW (долготы). Её центр - точка P, PM - радиус. Радиус PM (равный cos(pitch)) обозначим за R.
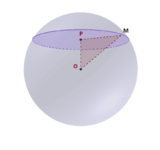
Рассмотрим эту окружность:
Для удобства повернём на 90 градусов по ч.с. Отметим случайное значение YAW, например точку K. Найдём точки синуса и косинуса.
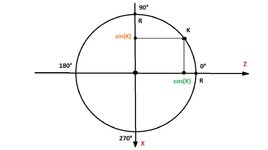
Ось X перевернута, значит синус нужно домножить на -1.
Получаем координаты X и Z нашего вектора взгляда:
X = -sin(yaw)
Z = cos(yaw)
Не забываем домножить на R, потому что окружность не единичная.
Получаем формулы для нахождения вектора взгляда:
X = -sin(yaw) * R = -sin(yaw) * cos(pitch)
Y = -sin(pitch)
Z = cos(yaw) * R = cos(yaw) * cos(pitch)
Вектор взгляда может пригодиться, если вы хотите запускать снаряд в направлении взгляда игрока и спавнить снаряд перед лицом игрока, чтобы снаряд не столкнулся с игроком который его запустил. Также необходим для рейкаста (перемещения по лучу взгляда в основном для проверки пересечения/близости луча взгляда и сущности/блока).
Для понимания потребуются некоторые знания из тригонометрии, поэтому в первой части я расскажу про тригонометрическую окружность, синус и косинус. Если уверен в своих знаниях - пропускай её.
Часть I. Начала тригонометрии.
Тригонометрическая окружность - это единичная окружность (окружность с радиусом 1) с центром в начале координат.

Какой угол (по величине) показан на правой окружности?
приблизительно -45°
Возьмём единичную окружность, отметим на ней случайную точку P.
Проведём отрезок PA параллельно оси X, точка A лежит на оси Y.
Проведём отрезок PB параллельно оси Y, точка B лежит на оси X.

Синус - координата точки A на оси Y.
Косинус - координата точки B на оси X.
Т.е синус и косинус - это просто координаты любой точки, лежащей на единичной окружности.
Синус - координата на вертикальной оси, косинус - на горизонтальной оси (если оси расположены так как на рисунке).
Но что если радиус окружности не равен 1?
С изменением радиуса окружности пропорциоонально изменяются и координаты точки.
- Чтобы найти координаты точки зная синус и косинус нужно умножить их на радиус.
- Чтобы найти синус и косинус точки зная координаты нужно разделить координаты на радиус.
Чему равен косинус этого угла?

0.5 (1/R = 1/2 = 0.5)
Часть II. Что такое вектор взгляда?
Вектор - это отрезок, имеющий направление, т.е начало и конец.

Единичный вектор - это вектор, длина которого равна 1.
Координатами вектора являются значения, сместившись на которые из начальной точки вектора (т.е прибавив их к координатам точки начала), мы окажемся в конечной точке вектора. Если начало вектора находится в начале координат, координаты вектора и координаты его конечной точки совпадают. Если начало не находится в начале координат, то чтобы найти координаты вектора нужно от координат конечной точки отнять координаты начальной.
Пример 1: есть вектор AB: A(0; 0), B(1; 3). Тогда AB{1-0; 3-0} = AB{1; 3}.
Пример 2: есть вектор CD: C(1; 1), D(-2; 3). Тогда CD{-2-1; 3-1} = CD{-3; 2}.
Вектор взгляда - это единичный вектор в трёхмерном пространстве, имеющий координаты, сместившись на которые точка будет находиться на луче взгляда.
Другими словами,
Вектор взгляда - это координаты для осей XYZ, на которые нужно сместиться, чтобы пройти единицу расстояния в направлении взгляда.

Часть III. Как получить вектор взгляда?
Получить вектор взгляда - значит найти координаты на которые нужно сместиться по осям XYZ, чтобы пройти единицу расстояния в направлении взгляда.
Для начала получим YAW и PITCH, вытащив значения из "Игровое значение" -> "Текущее направление взгляда".

PITCH и YAW измеряются в градусах.
PITCH - это поворот вниз-вверх
- Отсчёт: -Y (90°) +Y (-90°) (-90° .. 90°).
YAW - это поворот влево-вправо
- Отсчёт: +Z (0°/360°) -X (90°) -Z (180°) +X (270°) (0° .. 360°).
Так как длина вектора взгляда равна 1 (не меняется), набор всех возможных точек (концов векторов) образуют сферу (т.к сфера это по определению набор равноудалённых точек в трёхмерном пространстве).
На этой сфере PITCH - широта, а YAW - долгота (если вам это как-то поможет).

Рассмотрим PITCH (широту) на плоскости YA (см левую часть).
A - луч, который может лежать на оси X или Z, а может и не лежать, его местоположение зависит от YAW. Смотря на предыдущую картинку несложно представить, как эта полуокружность вращается вокруг оси Y с изменением YAW.

Для удобства перевернём картинку (см. правую часть). На полуокружности возможных значений PITCH находится точка M - случайное значение PITCH. Найдём значение синуса. Как можно видеть, оно лежит на перевёрнутой оси Y. Поэтому, для нахождения координаты Y вектора, его нужно домножить на -1 (это понятно ещё отсюда: "-Y (90°) +Y (-90°)" - в майнкрафте "вверх" это под отрицательным углом)
Итак, координата Y вектора взгляда найдена: -sin(pitch)
Теперь найдём точку косинуса, а точку sin(M) обозначим буквой P.
Можно заметить что длина отрезка PM = cos(M) = cos(pitch).

PM - это радиус окружности, которая получится на сечении сферы плоскостью XZ (горизонтальной плоскостью) в точке Y равной P. Сечение это то, что находится в секущей плоскости.
Фиолетовым выделена окружность, которая получится на сечении. Это окружность всех возможных значений YAW (долготы). Её центр - точка P, PM - радиус. Радиус PM (равный cos(pitch)) обозначим за R.

Сообщение объединено:
Рассмотрим эту окружность:

Для удобства повернём на 90 градусов по ч.с. Отметим случайное значение YAW, например точку K. Найдём точки синуса и косинуса.

Ось X перевернута, значит синус нужно домножить на -1.
Получаем координаты X и Z нашего вектора взгляда:
X = -sin(yaw)
Z = cos(yaw)
Не забываем домножить на R, потому что окружность не единичная.
Получаем формулы для нахождения вектора взгляда:
X = -sin(yaw) * R = -sin(yaw) * cos(pitch)
Y = -sin(pitch)
Z = cos(yaw) * R = cos(yaw) * cos(pitch)
Последнее редактирование: